- Deckblatt
-
Editorial
-
Was ist das: Träume und Wahrheiten?
| | -
Praefrontal
-
The (Somewhat Unexpected) Importance of Dreams in Science
-
Des Gedankens neue Kleider
zeigt auf, wie ein unachtsamer Gebrauch von Sprache unsere Gehirne buchstäblich zum Träumen anregen kann. -
Moderne Posten
erklärt, was das Verhalten in sozialen Netzwerken damit zu tun hat, wie wir uns und unsere Mitmenschen sehen. -
Der klägliche Intellekt
beleuchtet Nietzsche als Erkenntnistheoretiker
-
The (Somewhat Unexpected) Importance of Dreams in Science
-
Internationale Perspektiven
-
El significado de mi emigración
Die Bedeutung meiner Auswanderung | -
Equality, Truth, and the American Dream
examines the current situation of the LGBT community in America. -
Art, Theory, and the Link of Dreams and Reality in the 20th Century
-
Frege e il progetto del logicismo
Frege und das Projekt des Logizismus |
-
El significado de mi emigración
-
Vom Wesen der Dinge
-
Inspiration für Ideen
untersucht Träume als Impulsgeber für Kreativität in der Wissenschaft. -
The Constructed World of Mathematical Models
-
Freuds Theorie des Traumes
-
Marx, Wittgenstein und die Frage der Wahrheit
stellt zwei konkurrierende Theorien der Wahrheit gegenüber – und argumentiert, dass beide wichtig sind. -
Wahrheit im Strafprozess
über den Fall Calas und die Folgen für das europäische Rechtswesen.
-
Inspiration für Ideen
- In die Werkstatt
- Die Maschine
- Literatur
- Neue Wege
-
Amor fati
The Constructed World of Mathematical Models
Many of the scientists and engineers I have worked with have an illusory view of the way in which science generates knowledge. Using modern technology to perform complex computations, they assume that the intensive use of mathematical models and methods will lead them to the “discovery” of truths which are otherwise unobservable, and which will contribute to the further development of science, decision-making, and problem solving.
The psychologist Kenneth Gergen accurately describes this tendency when he writes that the: […] sciences have been enchanted by the myth that the assiduous application of rigorous methodology will yield sound fact – as if empirical methodology [which primarily includes statistical and econometric methods] were some form of meat grinder from which truth could be turned out like so many sausages.
1
Contrary to this belief, mathematical models construct their own reality through their formal architecture and the form of input data – in the same way that humans construct their own reality through their neurobiological nature. Mathematical models possess an internal truth which corresponds to the coherency produced by the rules of the formal system, but this does not mean that this truth corresponds to the external world. As a consequence, the hypotheses produced by the application of mathematical models can only possess a degree of plausibility with respect to their descriptive and predictive power.
This aspect of mathematical models is usually not taken into account. An inference formulated in mathematical language will almost always seem to be more valid than a statement in human language. Nonetheless, the comparison of the structure of mathematical models with the function of human cognition shows that both possess the same degree of validity.
Humans create inferences through a process which starts from the sensual and informational receptors of the person. The human sensory system is composed of the proprioceptors, exteroceptors, and interoceptors. Proprioceptors are the sensors which transmit information of the person’s motion and relative position of the body parts. Exteroceptors include all the receptors that react to the direct environmental stimuli, such as vision, taste, and touch. Finally, interoceptors are the effectors and receptors which signal bodily conditions such as hunger. These three groups of sensors constitute the connectors between the person and the world. According to the cognitive constructivist theory, for a human the world consists only of the totality of sensorial activity.2 The concrete function and specific type of the sensors as well as their coordination play a central role in the way that the world is reflected in the human organism, as the sensors provide all of the information which the nervous system processes. Organisms with different sensorial systems live in completely different realities, as the constructed worlds they are embedded in are constituted by the limits of their sensory systems. This idiosyncrasy of individual realities is further strengthened by the existing individual neural structure of the organism.
The person’s beliefs about the world are created through inferences, which are based on information sent by the sensors to the nervous system, the architecture, and structure of the nervous system, and its functional mechanisms. Hence, the reality of the person is constructed from a limited interaction of the person through her/his senses and her/his movement in the world. The sensory input is assimilated by the existing neural structure, a process which is imprinted in the plasticity of the neurons3, and then it is transformed into inductive inferences, through the synergy of semi-formal axiomatic and hypothetic-deductive human reasoning4, together with the intuitive operations5 and emotional forces6 of the human mind (fig. 1 a).
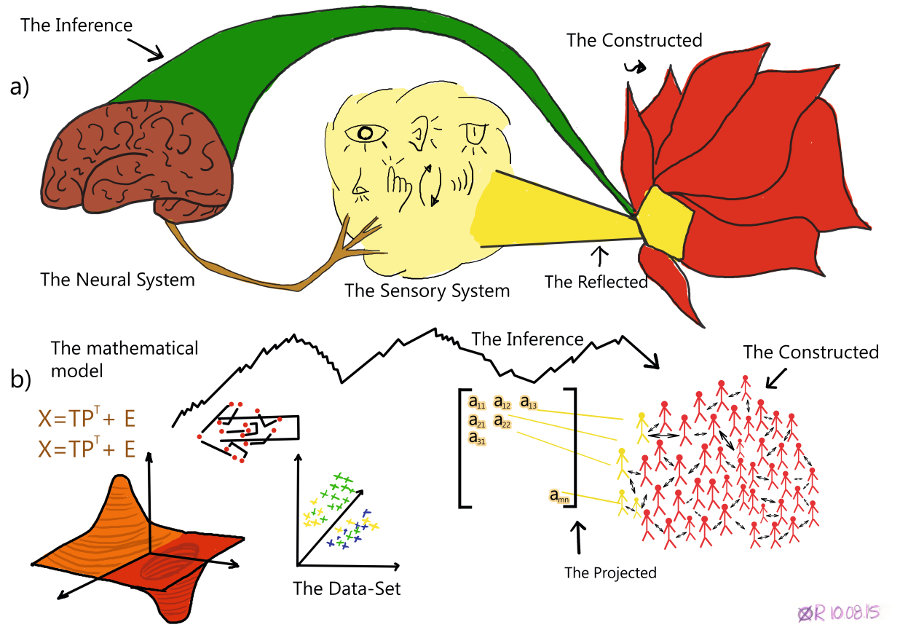
Hence, everybody constructs their own reality tied to their personal history, within the capacities of the human brain. Each person and each animal has a different perceived reality. Thus, a universal notion of truth cannot exist, as the limits of the human do not allow it. Even if more than one person agree that something is true, it is true only in the shared constructed reality they live in.
The human inferences seem to have an absolute validity only in the person’s constructed world, which is built out of a small number of fundamental elements using the concrete tools of the human brain. Consequently, there is no necessity that those inferences are going to be valid when applied in a different, more complex world. Hence, in no case is the claim justified that they could be characterized as true, as truth possesses an essence of absoluteness, which can never be acquired by the human mind.
Mathematical inferences have a similar structure to the inferences produced by human thought (fig. 1 b). A mathematical model is fed with a data-set in order to process it and derive a result. This data-set constitutes the only connection of the model to whatever it is the model describes. Moreover, the data-set works as a projection of the described entities on a constructed space with a specific quantitative and qualitative form. Any result is thus solely linked with this limited projection, as the mathematical model can only “perceive” this dimension of the world. Furthermore, the architecture of the mathematical model strongly influences the capabilities of each model and can pose strong restrictions in their predictive powers.
Despite this, mathematical models are broadly treated as true descriptions of the world: A popular view that prevails in the scientific community in the discussion about the power and reliability of data-intensive science is that so-called Big Data* models can discover true and precise correlative relations in the social world.
Data-intensive science claims that it can overcome the limitations of scientific theories and provide inferences with “unprecedented fidelity”.7 This view is based on the assumption that the input data-set contains all data.8 Something which does not hold, but it is assumed, as the huge number of data is adequate to overcome problems of ordinary statistics. Moreover, the inherent information of sufficiently large datasets exceeds by far the information that can be incorporated in a simple econometric model. Ideally, the model can possess the total projection of the world and consequently detect all correlative relations in it.
There are problems with this assumption. One is that the question “Can someone really gather all data of the world?”, is of metaphysical nature and is connected with the limits of the human. Another has to do with the qualitative difference between the projected data and the world under investigation. The way that the data is chosen to be quantified can influence the result of any mathematical model. A simple formulation of this problem is this: If a variable is described in the model as nominal, ordinal, or purely quantified, it always can have an effect on the final result. A variable is nominal when it does not have a numerical value. Take, for example, the color of a car. An ordinal variable ranks something according to given criteria (think of the hierarchy in a company). Purely quantified variables are attached to a numerical scale (think of the speedometer of a car). Ordinal and nominal variables are of qualitative nature. In order to be inserted in a mathematical model, an ordinal or nominal variable must be assigned a number. This can only be done by subjective criteria, there is no formal rule. As a consequence, different quantifications of these variables lead to different modeling results.
This problem is directly linked to the nature of data and the act of classification, as well as to the question whether or not everything that exists in the world can be described with numbers.
Moreover, the proponents of Big Data often do not take into consideration the structure of the mathematical methods used to produce the inferences. Data intensive models are based on econometric and statistical methods, which are not magical tools for the production of knowledge. The violation of inherent assumptions in a model can lead to spurious results, making the selection of the proper method a very complicated task. Even with one and the same data-set, the use of a slightly different mathematical model can lead to a major change in the final prediction.9
Furthermore, these models face restrictions coming from mathematics and the limits of matrix calculus. A typical issue in some econometric models is multicolinearity, which comes up when two or more variables have an almost linear relation to each other. This becomes a problem because the model requires the inversion of the data matrix, a process which includes dividing by 0 – an operation which is undefined in arithmetic.
The same mathematical property was the reason why Henri Poincare (1854–1912) came to the conclusion that Newton’s differential equations for the description of the motion of more than two celestial objects with gravitational interaction do not have an analytical solution.10A result which led to the development of the complex systems theory.
The discourse becomes more intense when the decisions that are based upon them have a major impact on the social life of humans and evoke radical changes in social structure. In economic science, the use of formal methods prevails as a necessity, because it is believed that in this way the field becomes rigorous and scientific,11 although the inferences made by these formal tools very often fail to make any valid predictions.12 This obsessive use of econometrical and probabilistic models ends up being problematic.
The most fundamental aspects of mainstream economics (concerning the structure of the market, of labor relations, and the way the state and social institutions should function in society) spring out of inferences based on some economic assumptions, simple mathematical models of few financial variables together with the famous ceteris paribus**. Thus, every time the models fail the excuse is that there was a political incident, or that a rare event occurred, etc. Still, these problems do not evoke any change in the way economic scientists handle their predictions. Economists keep on using the same methods with the same poor results, justified on the inherent truth of the models, ignoring that there might not exist any correspondence between the models’ results and the social interactions taking place.
Even if a model does describe the world accurately, it does not mean that we learn something true about the world. It merely signifies that the model used has a specific descriptive power under some specific conditions.
In political science, game-theoretic models are broadly used for the description of conflicts and bargaining. A case study which is often referred to the success of these methods is the “Cuban missile crisis” of 1962,13 when the threat of a nuclear war between the US and the USSR was highly probable. Many different variations of game-theoretic models have been applied to these events in order to show the descriptive power of the methods. But what is not analyzed is the way in which the starting conditions of the models are decided upon. Every “player” in a game has a payoff for a possible move she/he makes, which is chosen under some empirical assumptions from the scientist. According to these payoffs the nature and outcome of the game totally changes. Hence, that the models were calibrated a posteriori in a specific way, capable of describing a social interaction, does not mean that every application of the model in a similar situation will have the same success.
The difference between an epistemic model and the world also has to be kept in mind in cosmology. The idea of the Big Bang theory came from the application of the equations of general relativity theory and their extension by the physicist Friedman.14 The emergence of a mathematical singularity in the equations together with the investigation of empirical facts led to the creation of the Big Bang hypothesis. This does not mean that the Big Bang theory is true. The hypothesis is rather a construction that emerged from a mathematical model. As long as empirical evidence does not falsify it, it can be considered a descriptive hypothesis, and Friedman’s equations can be seen as plausible descriptions of the world.
In summary, mathematical models produce inferences which are only absolutely valid in their respective mathematical world. They face limitations in their structure and their results similar to the limitations of human thought. Although some in the scientific community do not accept this thesis, scientists should incorporate this perspective in their working assumptions.
It is necessary to overcome dogmatic formalism and claims of absolute truth in order to move forward and face new challenges in the scientific discourse.
- Kenneth J. Gergen, The social constructionist movement in modern psychology American Psychologist 40, no. 3 (1985), 273.
- Heinz von Foerster, On Constructing a Reality, in: Understanding Understanding: Essays on Cybernetics and Cognition (Springer Publishing Company, 2010), 211–227.
- Gisela Labouvie-Vief, Integrating emotions and cognition throughout the lifespan (Springer, 2015), 34.
- Jean Piaget, The psychology of intelligence (London: Routledge & Paul, 2005), ch. V.
- Ibid., ch. IV.
- Gisela Labouvie-Vief, 9.
- Chris Anderson, The End of Theory: The Data Deluge Makes the Scientific Method Obsolete (2008), http://archive.wired.com/science/discoveries/magazine/16-07/pb_theory (accessed: November 30, 2015).
- Wolfgang Pietsch, Aspects of theory-ladenness in data-intensive science, Philosophy of Science Assoc. 24th Biennial Mtg. Chicago, IL (2014), 7.
- Äozgäur Yeniay, A comparison of partial least squares regression with other prediction methods Hacettepe Journal of Mathematics and Statistics, no. 31 (2002). 99–111.
- Henri Poincare, New methods of celestial mechanics, vol. 3, National Aeronautics and Space Administration (ed.) (Springfield VA, 1967), 167, http://www.archive.org/details/nasa_techdoc_19670017950 (accessed: November 30, 2015).
- Geoff Hodgson, On the problem of formalism in economics, Voprosy Economiki, no. 3 (2006), 112–124.
- Nassim Nicholas Taleb, The black swan: the impact of the highly improbable (New York: Random House, 2007), ch. 11.
- Avinash K. Dixit and Susan Skeath, Games of strategy (New York: W.W. Norton, 2004), 471–496.
- Alexander Friedman, On the Curvature of Space, General Relativity and Gravitation, no. 31 (1999),1991–2000.


Feedback