Felix Reuß

Kurt Gödel, einer der bedeutendsten Logiker des vergangenen Jahrtausends, sagte im Jahr 1933 nach einem Treffen des Wiener Kreises zum Thema Sprache: „The more I think about language, the more it amazes me that people ever understand each other at all.“1 Dass also Sie, liebe Leserinnen und Leser, in der Lage sind die Thesen dieser Zeilen zu verstehen, kann bereits Auslöser für die freudige Verwunderung eines professionellen Logikers sein. Grundlegende Probleme der Kommunikation, die Sie beispielsweise gerade jetzt ganz automatisch lösen, überhaupt zu identifizieren und zu analysieren bereitet dieser Zunft von Wissenschaftlern noch heute große Schwierigkeiten.

Vergleichbar zu mathematischen Methoden versuchen sie dabei oft zentrale Fragestellungen in einzelne Aufgaben aufzuteilen und diese auf handhabbare Theorien zurückzuführen. Anstatt der Kommunikation mittels üblicher Sprachen, wie etwa Deutsch, Englisch oder Suaheli, vereinfacht sich das Problem erkennbar mit einer Einschränkung auf Kommunikation mittels leichter zu untersuchenden, nonverbalen, formalen Sprachen. Auch wenn diese Reduzierung der betrachteten Kommunikation zuerst radikal erscheint, ergibt sich ein breit gefächertes Forschungsfeld. So wird beispielsweise nahezu jedes naturwissenschaftliche, mathematische bzw. informationstechnische Wissen mithilfe von verschriftlichten mathematischen Formeln und dazu passenden Interpretationsmöglichkeiten kommuniziert. Der Zusammenhang zwischen eigentlichem kommunizierten Inhalt und der benutzten Verschriftlichungsart wird aber in keiner der spezifischen Fachdisziplinen gezielt untersucht.

Eine der für eben dieses Untersuchungsvorhaben notwendigen Arbeitshypothesen stammt aus der Semiotik: Jedem Kommunikationsprozess liegen jedem Kommunikationsteilnehmenden bekannte Codes, Zeichen und Regeln zugrunde.2 Gäbe es nämliche keine gemeinsame epistemische Formalisierungsrundlage, also allseits bekannte Verschriftlichungsvorlagen und Interpretationsvorschriften, so wäre eine intentionale Verständigung unmöglich und jegliches Übermitteln von fachspezifischen Inhalten und Formeln würde zu einem individuellem Erkenntnisgewinn bzw. -verlust verkümmern, welcher aus subjektiver Interpretation der kommunizierten Zeichen besteht.

In der wissenschaftlichen Disziplin Mathematik ist beispielsweise der zentrale Kommunikationsprozess das Vermitteln von Theoremen und Beweisen. Neben den für jede Kommunikation notwendigen semiotischen Grundlagen (Codes, Zeichen und Regeln) ist ein mathematisches Theorem zudem notwendigerweise von einem mathematischem Kalkül und der dazugehörenden ideengeschichtliche Tradition abhängig, damit ein intentionales Verständnis des Theorems überhaupt erst möglich ist.

Die erfolgreiche Vermittlung eines mathematischen Theorems konstituiert daher simultan zwei, den Kommunikationsteilnehmenden notwendigerweise bekannten Regelsammlungen (semiotisch und mathematisch), die in insgesamt drei verschiedenen Ebenen der mathematischen Kommunikation eingeteilt werden können:

• Die Inhaltsebene (Theorem).
• Den Interpretationsrahmen (Ideengeschichte) und Kontext (math. Kalkül).
• Die Zeichen („+“, „-“, „:“, etc.).

Bereits anhand eines einfachen mathematischen Gesetzes, wie exempli causa der Transitivität der Gleichheitsrelation bzgl. natürlicher Zahlen (aus A = B und B = C folgt A = C) kann aufgezeigt werden, inwiefern die verschiedenen Ebenen und Regelsammlungen der mathematischen Kommunikation voneinander abhängen. Eine standardisierte Variante dieses Gesetz zu formalisieren um es schließlich kommunizieren zu können ist beispielsweise:

Variante 1: (Standard) Seien A, B und C natürliche Zahlen, wobei A = B und B = C, dann ist auch A = C.

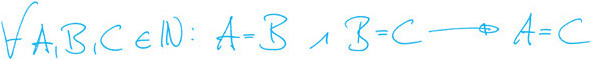
Die übliche (deutsche) Sprache, bzw. die dazugehörige moderne quantifizierte Formelschreibweise, bieten alleine sowohl keinen ausreichenden Kontext, als auch keinen brauchbaren Interpretationsrahmen um von der Darstellung des Gesetzes auf den eigentlichen Inhalt, also der Transitivität der Gleichheit von natürlichen Zahlen, zu verweisen. Ohne eine Vorstellung, wie Variablen mit natürlichen Zahlen etc. zusammen hängen, besteht der obige Satz hauptsächlich aus einzelnen Buchstaben, Zeichen und ein paar unzusammenhängenden Wörtern. Erst im Hinblick auf einen, nach der semiotischen Arbeitshypothese allen Kommunikationsteilnehmenden bekannten, mathematischen eindeutigen Kontext und Interpretationsrahmen, wie z.B. die Peano-Arithmetik, ist es möglich, den Satz bzw. die Formel mit dem Gesetz eindeutig zu identifizieren und damit zweifelsfrei zu kommunizieren.

Eine weitere Variante dieses Gesetz (bzgl. der Peano-Arithmetik) zu formalisieren und zu kommunizieren ist eine Verschriftlichung nach den Regeln der Begriffsschrift3 von Gottlob Frege:

Variante 2: (Begriffsschrift) [Abkürzungen wie oben]

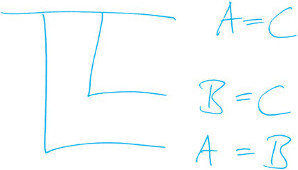
In die übliche (deutsche) Sprache übersetzt bedeutet dies: „Es ist beurteilbar, dass aus der Gleichheit der Zahlen A und B und der Gleichheit der Zahlen B und C die Gleichheit der Zahlen A und C geschlossen werden kann.“ Die Bejahung dieses Urteils, also „es ist wahr, dass aus der Gleichheit der Zahlen A und B und der Gleichheit der Zahlen B und C die Gleichheit der Zahlen A und C geschlossen werden kann“ wird mithilfe der Begriffsschrift zu:

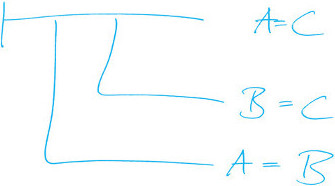
Die Begriffsschrift gilt insgesamt als die erste (zweidimensionale) Darstellungs- bzw. Verschriftlichungsmethode von Formeln der Prädikatenlogik zweiter Stufe. Hierdurch besitzen die beiden bisher aufgezeigten Varianten eine Gemeinsamkeit: Die herangezogenen Verschriftlichungsmethoden (die übliche (deutsche) Sprache inkl. quantifizierter Formelschreibweise und die Begriffsschrift) können jeweils Formeln der Prädikatenlogik zweiter Stufe darstellen. In diesem Sinne sind sie also gleich mächtig. Ein wesentlicher Unterschied, neben der offensichtlichen Zweidimensionalität der zweiten Variante, ist der veränderte Kontext und Interpretationsrahmen. Während Ausdrücke der ersten Formalisierungsvariante explizit mathematische Strukturen beschreiben, stellen Ausdrücke der Begriffsschrift potentielle Urteile (keine Dinge) dar, die entweder als wahr oder falsch gelten können.

Ein weiterer Unterschied zwischen diesen Varianten ist die implizite Bezugnahme auf ein logikbetreibendes bzw. urteilfällendes Subjekt. Während die übliche (deutsche) Sprache in Verbindung mit der Peano-Arithmetik als Kontext eine mathematische Struktur beschreibt und somit unabhängig von jeglichem metasprachlichen Subjektbezug ist, benötigt die Begriffsschrift als Voraussetzung die Existenz eines urteilfällenden Subjekts, da sie ausschließlich auf Urteilen aufbaut und keinen objektiven Bezugsrahmen besitzt. Die Peano-Arithmetik gibt hier dem jeweiligen Subjekt nur den Rahmen vor, in dem das Urteil gefällt wird. Der eigentlichen Interpretationsvorschrift der ersten Kommunikationsvariante stellt die Begriffsschrift also den metasprachlichen Subjekt bzw. Urteilsbezug entgegen, verliert aber auch die metasprachliche Objektivität. Anstatt wissen zu müssen, wie beispielsweise A=B interpretiert wird, ist es notwendig zu wissen, wie über A=B geurteilt werden kann.

In Freges Wissenschaftsauffassung gelten Ausdrücke der Begriffsschrift, also potentielle Urteile, als grundlegender Gegenstand. Da diese Urteile in einem Kontext eingeordnet sind und damit in mögliche Rahmen für eine Urteilsfindung, ist somit Logik als theoretisches Fundament aller Wissenschaften fixiert. Wird die Begriffsschrift als Formalisierungs- bzw. Verschriftlichungsmethode in Freges Sinn benutzt, geht damit auch notwendigerweise die Entscheidung für eine reduktionistische Wissenschaftsauffassung einher.

Vergleichbar dazu legt Spencer-Brown die Mathematik als Ausgangspunkt einer reduktionistischen Auffassung von Wissen fest. Logik ist für ihn dabei lediglich eine Anwendung bzw. Interpretation seines mathematischen Indikationskalküls.4 Dieser Kalkül beruht dabei auf der grundlegenden Idee des Unterscheidens und Indizierens. Ein Zustand, wie z.B. „wahr“, kann in diesem Kalkül beispielsweise nur durch eine Indizierung desselben von seinem Gegenteil, hier „falsch“, unterschieden werden. Die dritte Variante zeigt also eine Darstellungsweise des Gesetzes über die Transitivität der Gleichheit von natürlichen Zahlen mithilfe Spencer-Browns für die Aussagenlogik interpretiertem (fAi) Indikationskalküls.

Variante 3: (Laws of form) [Abkürzungen wie oben]

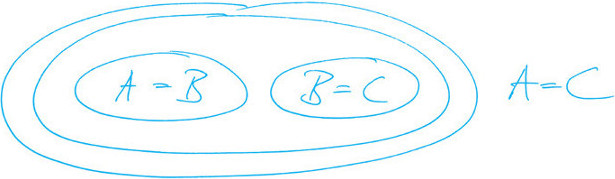
Elementare Aussage des (fAi) Indikationskalküls sind hierbei wie folgt zu verstehen, wobei es nur darauf ankommt, was in einem Kreis steht und was außerhalb:

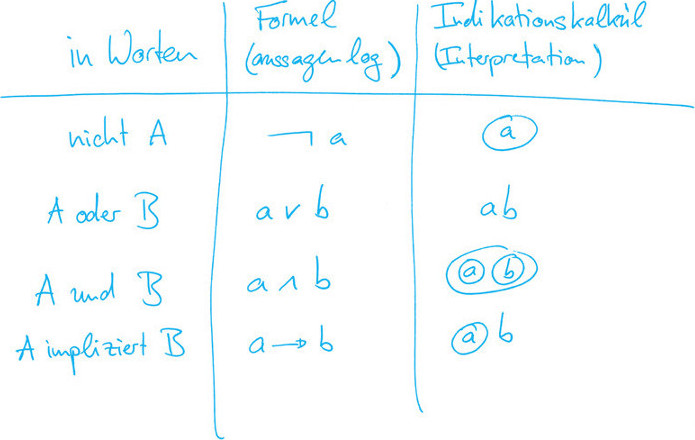
Zudem bezeichnen Großbuchstaben Aussagen und der jeweilige Kleinbuchstabe deren Wahrheitsgehalt.

Neben der gemeinsamen Zweidimensionalität der Darstellungsweisen teilen die letzten beiden Varianten, im Gegensatz zur ersten, eine starke semantische Auffassung des Interpretationsrahmens und Kontextes. Spencer-Browns (fAi) Indikationskalkül trennt, ebenso wie die Begriffsschrift Freges, klar zwischen beschriebener Struktur und semantischer Bedeutung der eigentlichen Aussage. Eine Aussage A ist im (fAi) Indikationskalkül als eine Art Name (Index) für ihren Wahrheitswert a zu verstehen und besitzt daher, äquivalent zu den potentiellen Urteilen in Freges Begriffschrift, keinen unmittelbaren Bezug zur Außenwelt. Spencer-Brown nimmt, ebenso wie Frege, Bezug auf ein logikbetreibendes bzw. unterscheidendes und indizierendes Subjekt, da die dem Indikationskalkül zugrunde liegenden Ideen des Unterscheidens und Indizierens von ihm als nicht unabhängig von einem Unterscheider bzw. Indizierer aufgefasst werden. Ebenso ist die Wahl der aussagenlogischen Interpretation des (mathematischen) Indikationskalküls für ihn willkürlich.

Im Gegensatz zu Freges Begriffsschrift indizieren Aussagen Spencer-Browns (fAi) Indikationskalküls jedoch den Zustand ’wahr’ oder ’falsch’ und sind nicht als ’wahr’ oder ’falsch’ zu beurteilen. Ein Unterschied zwischen dieser Variante und den ersten beiden ist die eindeutige Leserichtung der verschriftlichten Formeln aufgrund der jeweils verwendeten Zeichen. Während die ersten beiden Varianten Leserichtungen „von links nach rechts“ bzw. „von links nach rechts und unten nach oben“ voraussetzen und damit eine eindeutige Reihenfolge festlegen, legt die Leserichtung „von innen nach außen“ der letzten Variante keine eindeutige Reihenfolge fest. Eindeutige Übersetzungen bzgl. des syntaktischen Aufbaus und somit auch eindeutige Interpretationen von Aussagen des (fAi) Indikationskalküls in beispielsweise der Begriffsschrift oder üblichen Sprachen sind damit unmöglich. Mathematische Strukturen, sowie Gesetze können demgegenüber dennoch eindeutig dargestellt werden.

Eine Krux der Kommunikation anhand formaler Sprachen ist also, dass bereits Variationen einzelner Verschriftlichungsmethoden nicht nur rein syntaktische und darstellungsbedingte Unterschiede erzeugen können, sondern auch wesentliche inhaltliche Abweichungen. Die Form eines Theorems ist also ein Teil desselben. Allgemein ausgedrückt kommt es also nicht nur darauf an, was kommuniziert wird, sondern auch wie.

„Den Stoff sieht jedermann vor sich, den Gehalt findet nur der, der etwas dazu zu tun hat, und die Form ist ein Geheimnis den Meisten.“5